Julkaisutyypit

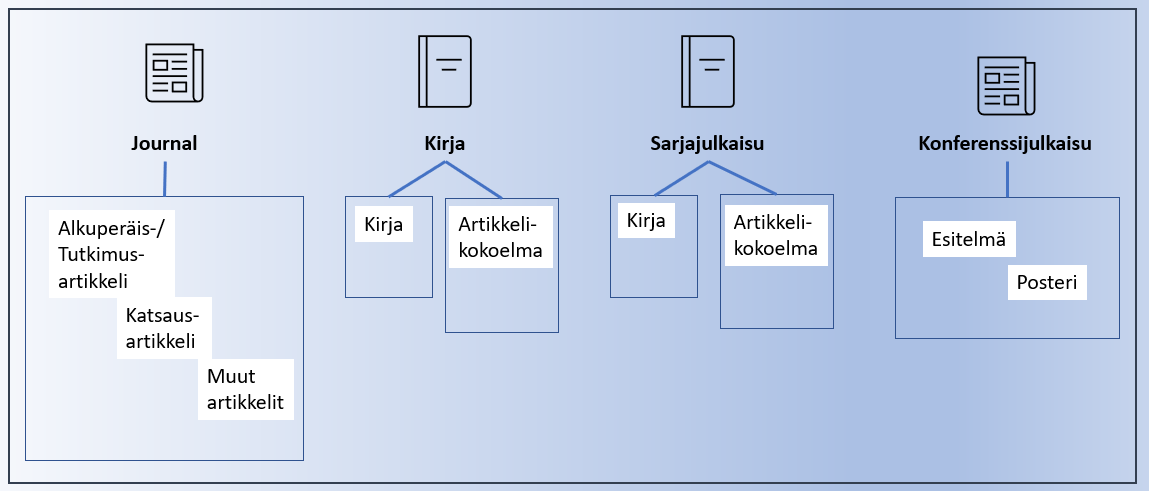
Yleisin tapa julkaista tutkimustietoja on artikkeli tieteellisessä lehdessä. Myös kirjat, sarjat ja konferenssijulkaisut ovat keskeisiä julkaisukanavia.

Artikkelit raportoivat uusia tutkimustuloksia

Tieteellisen lehden (journal) sisältö jakautuu yksittäisiin artikkeleihin. Artikkeleita on kahta päätyyppiä: alkuperäisartikkeleita ja katsaus- eli review-artikkeleita.

Varsinaisten tutkimusartikkelien lisäksi tieteelliset lehdet voivat sisältää myös erilaisia katsauksia, uutisia, kirjeitä ja keskustelua.

Arkikielessä tieteellisiä lehtiä kutsutaan usein sarjoiksi, mikä voi aiheuttaa sekaannuksia (ks. alla sarjajulkaisuista). Jotkut tutkijat puhuvat myös ’journaaleista’. Esimerkki tieteellisestä lehdestä:

Alkuperäisartikkeli

Alkuperäisartikkeli (original/research article/paper) sisältää joko täysin uusia tutkimustuloksia tai vanhojen tulosten uutta tulkintaa.

Alkuperäisartikkeli on lyhyehkö, keskimäärin 7-10 sivun mittainen esitys jostain kyseisen lehden tieteenalaan liittyvästä selkeästi rajatusta ongelmasta. Pelkästään alkuperäisartikkeleita lukemalla on hankalaa saada yleiskäsitystä laajemmista aiheista ja tietämyksen tasosta tieteenalalla.

Katsausartikkeli

Katsausartikkelit (review article) kokoavat yhteen aikaisempien tutkimusten tuloksia.

Katsausartikkeleita laativat tieteenalojen kokeneet asiantuntijat. Katsausartikkelia varten käydään läpi kaikki tärkeimmät kyseiseen aiheeseen liittyvät alkuperäisartikkelit. Katsaukset ovat yleensä pitkiä, kymmenien sivujen mittaisia, ja niissä on kattavat lähdeluettelot. Katsausartikkelit ovat tunnusomaisia aloilla, joissa tutkimusta samasta aiheesta kertyy monista yksittäisistä tutkimuksista ja hieman eri näkökulmista. Matematiikassa tällainen tutkimus on yleensä soveltavaa tai vaikkapa opetukseen liittyvää.

Termi review esiintyy matematiikan tiedonlähteissä useammin hieman toisessa merkityksessä. Alan keskeinen tiedonlähde, MathSciNet-tietokanta, sisältää (ulkopuolisen) arvion ja kuvailun kunkin julkaisun (artikkeli, kirja) sisällöstä. MathSciNet onkin eräänlainen käyttöliittymä julkaisusarjalle, jonka nimi on Matematical reviews. Vastaava käytäntö on toisessa matematiikan alan tietolähteessä, zbMATH.

Current events bulletin on matemaatikkojen versio katsausartikkeleita sisältävästä lehdestä. Myös muissa lehdissä ilmestyy katsausartikkeleita muiden seassa. Alan uusimpia käänteitä esittelevä artikkeli on nimetty vaikkapa: Recent advaces in ….

Sarjat kertovat tietyssä organisaatiossa tehdystä tutkimuksesta

Julkaisusarjat ovat erityisesti tutkimuslaitosten ja muiden julkisorganisaatioiden tavallinen väylä työn tulosten julkistamiseen ja siten tärkeitä tiedonlähteitä.

Esimerkiksi väitöskirjat julkaistaan Suomessa yliopistojen sarjoissa lähes poikkeuksetta.

Sarja ilmestyy tietyllä nimellä ja toistuvina osina kuten lehtikin. Sarjat ja lehdet ovatkin yhteiseltä nimeltään kausijulkaisut. Sarjan osat eivät kuitenkaan välttämättä ilmesty yhtä säännöllisin välein kuin lehtien numerot. Sarjan osa ilmestyy, kun julkaisu on valmis. Osien määrä per vuosi voi sekin vaihdella. Yleensä eri osilla on omat teemansa tai aiheensa kirjan tapaan.

Kaikkein ”tieteellisimmät” uudet tulokset julkaistaan nykyisin mieluiten artikkelina vertaisarvioiduissa lehdissä, mutta sarjajulkaisujen kautta välitetään edelleenkin runsaasti raportti-, selvitys- ja casetyyppistä tutkimustietoa. Sarjajulkaisu ei useinkaan ole vertaisarvioitu, mutta silti käyttökelpoinen lähde.

Viime vuosina paljon sarjajulkaisuja on siirtynyt vain verkossa julkaistaviksi, mikä on heikentänyt niiden löytyvyyttä esim. kirjastotietokannoista. Sarjoja löytää paremmin eri organisaatioiden omista verkkojulkaisujärjestelmistä. Hakukoneiden tuloksiin voi myös tarttua sarjajulkaisuja.

Konferenssijulkaisut ovat nopea tapa julkaista uusia asioita

Uusia tutkimustuloksia esitellään aluksi tieteellisissä kokouksissa. Kokouksessa pidetyt esitelmät tai niiden lyhennelmät sekä mahdollisesti posterit kootaan yleensä kokousjulkaisun muotoon. Tämä pyritään tekemään mahdollisimman lyhyellä viiveellä, usein jopa ennen kokouksen alkua.

Kansainvälisten kokousten julkaisut tunnistaa usein siitä, että niiden nimessä esiintyy sana proceedings.

Konferenssi voi olla säännöllisesti vuosittain järjestettävä, tai yksittäinen kokous. Konferenssijulkaisu on muodoltaan painettu- tai verkkokirja. Konferenssilla voi olla myös oma julkaisusarja. Konferenssiartikkeleita voidaan julkaista myös lehdissä.

Kirjat kertovat aiheestaan laajasti

Kirja eli monografia kirjoitetaan yleensä siinä vaiheessa, kun tietämys aiheesta on yleisesti hyväksyttyä ja vakiintunutta. Kirjan julkaiseminen vie aikaa, ja kirjatiedoilta yleensä myös odotetaan tiettyä pysyvyyttä.

Kirja esittelee ilmiön taustat ja antaa kokonaiskuvan aiheesta.

Kokoomateos

Kokoomateoksella tarkoitetaan kirjaa, joka on toimitettu (edited) useamman kirjoittajan erillisistä artikkeleista. Toimittaja (editor) voi olla myös jonkin artikkelin kirjoittaja (author), mutta välttämätöntä tämä ei ole.

Hakuteokset tiivistävät asioita

Käsikirjat, tietosanakirjat, ensyklopediat (handbooks, encyclopedias) sisältävät yleis- tai alakohtaista tietoa tiivistettynä lyhyiksi artikkeleiksi. Näistä kirjoista löytää hyvin mm. määritelmiä, teorioita, matemaattisia todistuksia, aihealueen historiaa sekä hyviä lähdeteoksia.

Seuraava sivu: Tieteelliset julkaisut eri aloilla.